closed sets and limit points Let hat S be the set of all limit points of S Prove that hat S is a closed set Proof Suppose x 0 is a limit point of hat S Then given varepsilon 0 there exists x in hat
Closed Sets and Limit Points Note In this section we finally define a closed set We also introduce several traditional topological concepts such as limit points and Exercise open case Z Y open U open in X s t Z Y U Z is open in X because Y U are open To check Y A is the closure verify it is the smallest closed set in Y containing A Y A
closed sets and limit points

closed sets and limit points
https://i.ytimg.com/vi/Ze8zsr1jeAI/maxresdefault.jpg
401 8 Open And Closed Sets And Their Points YouTube
https://i.ytimg.com/vi/CeKmZ_LBeUg/maxresdefault.jpg

General Topology Prove That A Closed Set Contains All Its Limit
https://i.stack.imgur.com/rTcn1.jpg
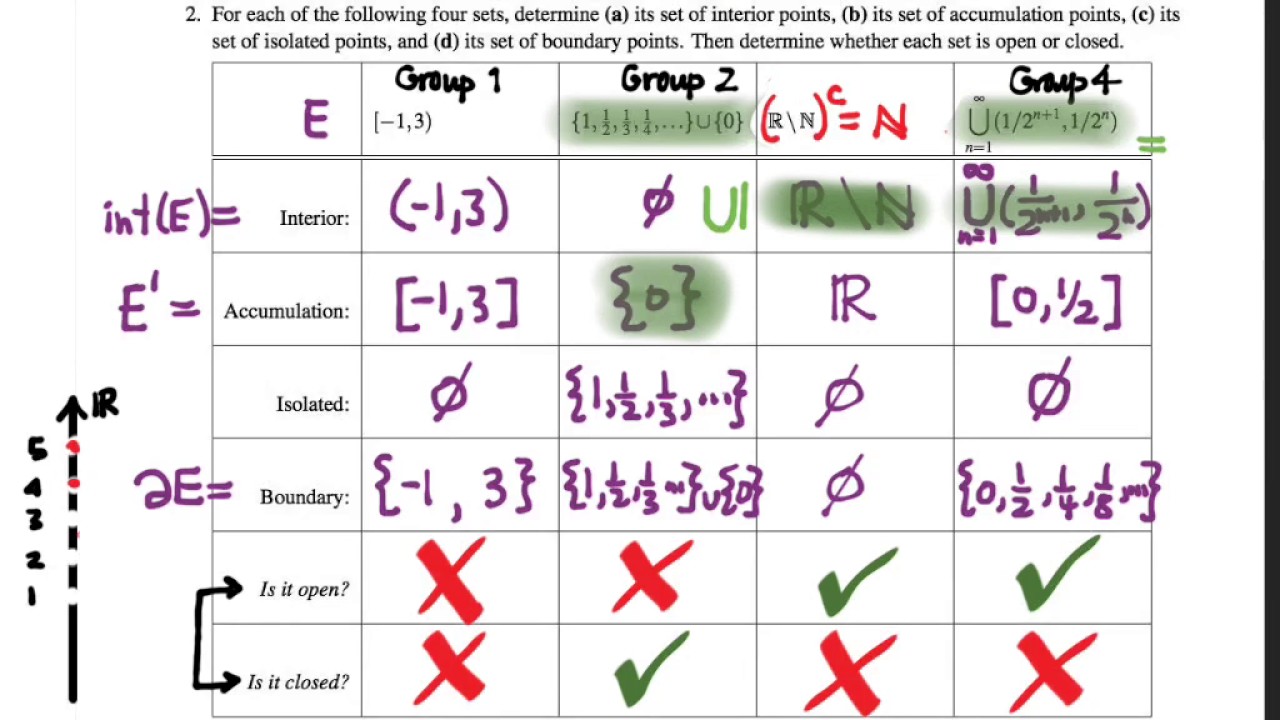
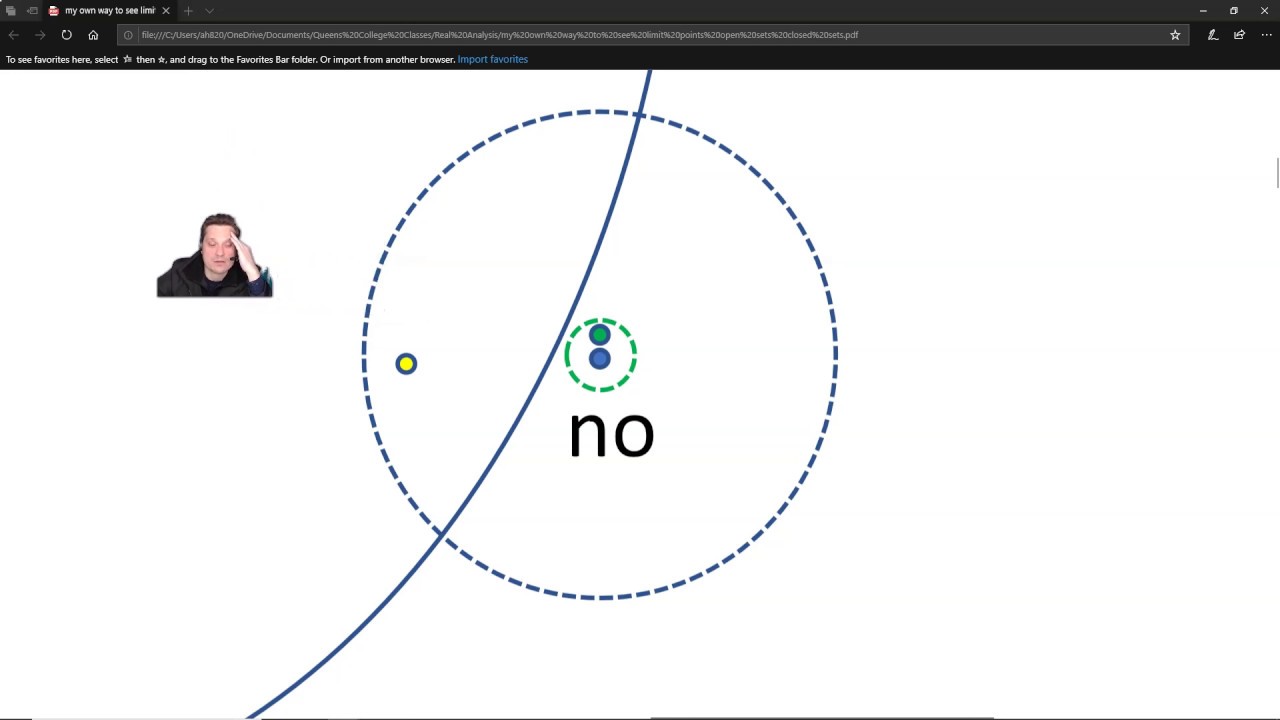
Limit points are not the same type of limit that you encounter in a calculus or analysis class but the underlying idea is similar Informally a point in a metric space is a limit point of some subset if it is arbitrarily close to other points in The limit points of a set S are those numbers that are limits of sequences of members of that set A set is closed if it contains all its limit points Notice that 0 by definition is not a
Definition limit points We call a point x in mathbb R a limit point of a set A subset mathbb R if for every epsilon 0 there exists a in A a neq x such that a in x In geometry topology and related branches of mathematics a closed set is a set whose complement is an open set 1 2 In a topological space a closed set can be defined as a
More picture related to closed sets and limit points
Concepts Behind Limit Points Open Sets Closed Sets And Boundary
https://i.ytimg.com/vi/FP2PrBI1LQY/maxresdefault.jpg

DIFFERNTIAL GEOMETRY Quick Review On Closed Sets And Limit Points
https://i.ytimg.com/vi/KjKvdww0OBQ/maxresdefault.jpg

Real Analysis Limit Points Closure Isolated Points Mathematics
https://i.stack.imgur.com/gfFeN.png
Here are two facts about limit points 1 A point x is a limit point of S if and only if every open ball containing it contains at least one point in S which is not x 2 A subset of a metric space X is closed if and only if it A set Cin X d is closed if it contains all of its limit points Note that every point in Cis a limit point of C take the constant sequence x x x the point of being closed is that the opposite
In words the interior consists of points in Afor which all nearby points of X are also in A whereas the closure allows for points on the edge of A The set of interior points in D constitutes its interior int D i n t D and the set of boundary points its boundary D D D D is said to be open if any point in D D is an interior point and

Real Analysis Is The Intersection Of A Set And Its Set Of Limit
https://i.stack.imgur.com/mh8fd.png

PROOF TECHNIQUES FOR CLOSED SETS AND LIMIT POINTS YouTube
https://i.ytimg.com/vi/y2Xw9gVv5fI/maxresdefault.jpg
closed sets and limit points - Limit points are not the same type of limit that you encounter in a calculus or analysis class but the underlying idea is similar Informally a point in a metric space is a limit point of some subset if it is arbitrarily close to other points in