accumulation point of a set An accumulation point is a point that is infinitely close but not necessarily a member of a set or sequence That is to say p is an accumulation point of A if for any distance no matter how small there will be an element of A other than p itself within that distance from p fleablood Nov 28 2022 at 0 32 Add a comment 2 Answers Sorted by
If every open set containing x contains infinitely many points of S then x is a specific type of limit point called an accumulation point of S If every open set containing x contains uncountably many points of S then x is a specific type of limit point called a condensation point of S A compact set is a subset of R that is closed and bounded and has the property that every sequence in it has a convergent subsequence Learn the definition theorem and examples of compact sets in analysis
accumulation point of a set

accumulation point of a set
https://i.ytimg.com/vi/fEFmv_UKTfo/maxresdefault.jpg

Real Analysis If A Point p Is An accumulation Point Of A Set S Then
https://i.stack.imgur.com/G9O4b.jpg
Solved 28 A Number X Is Called An Accumulation Point Of A Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/c31/c314da94-ad33-482f-811f-62ea223436a4/image
An accumulation point is a point that is the limit of a sequence or a map Learn how to identify accumulation points and see related topics and applications in calculus and dynamical systems Point p is accumulation point of a set S if every punctured neighborhood of the point p contains points of S In other words if there exists sequence x n subset S that converges to p Set S left lbrace sin dfrac 1 n cos dfrac 1 n right rbrace n in mathbb N left lbrace sin 1 cos 1 sin dfrac 1
We will now define a very important type of point of a set in a topological spaces known as accumulation points Definition Let X be a topological space and let A X A point x An accumulation point of a set in a topological space is a point that has a point of the set in any neighbourhood Learn the definition examples and distinction from proximate and complete accumulation points
More picture related to accumulation point of a set
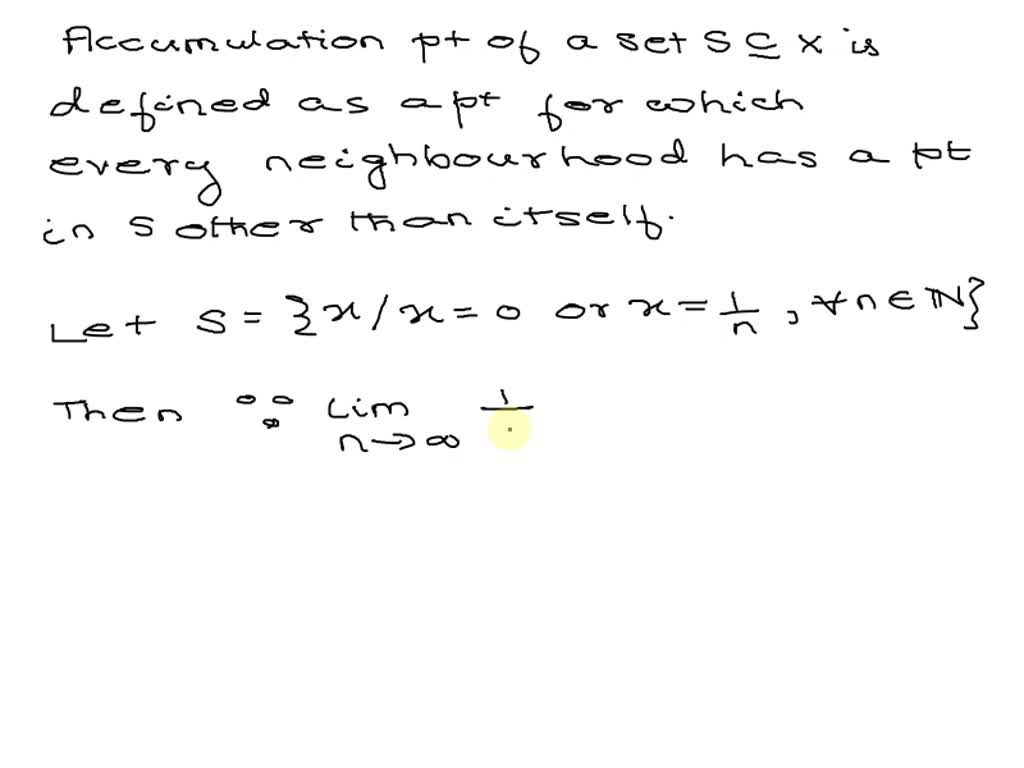
SOLVED Show That Every Point Of A Set Is Either Isolated Or A Point Of
https://cdn.numerade.com/ask_previews/6e2cf83c-ec91-47fb-b376-3daa34477cb7_large.jpg

Examples Of Accumulation limit Points From Basic Topology With Sets
https://i.ytimg.com/vi/rIZrElqOIEo/maxresdefault.jpg

401 8 Interior Accumulation Points Open And Closed Set YouTube
https://i.ytimg.com/vi/U1XDWeeDBrQ/maxresdefault.jpg
An accumulation point can be considered as a limit of a sequence of points from the set approaching that point without ever reaching it In the complex plane accumulation points play a key role in determining convergence and compactness which are essential concepts in analysis Determine all of the accumulation points for a n Notice that a n frac n 1 n 1 frac 1 n We know that lim n to infty 1 frac 1 n 1 and so a n is a convergent sequence By theorem 1 we have that all subsequences of a n must therefore converge to 1 and so 1 is the only accumulation point of a n
[desc-10] [desc-11]

Limit Point Or accumulation Point Of A Set With Example Derived Set
https://i.ytimg.com/vi/hXPI8Lw3kB8/maxresdefault.jpg
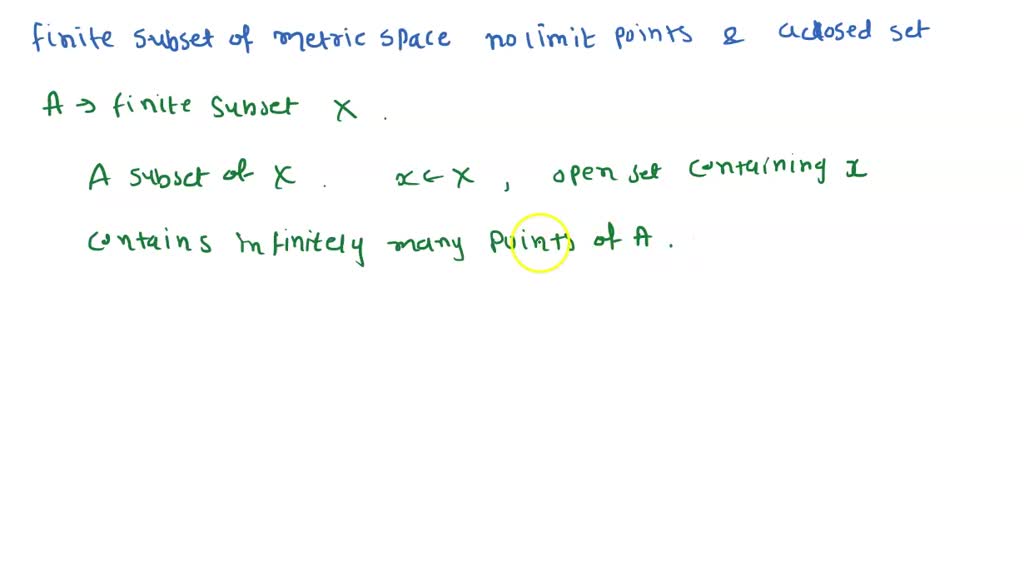
SOLVED Show That Every accumulation Point Of A Set That Does Not
https://cdn.numerade.com/ask_previews/92978800-c19c-42bc-b7a8-55dedf8272df_large.jpg
accumulation point of a set - An accumulation point is a point that is the limit of a sequence or a map Learn how to identify accumulation points and see related topics and applications in calculus and dynamical systems
