4 pi r 2 In my textbooks and lectures I m a second year physics student I often come across statements such as dV 4 pi r 2dr text can be thought of as the spherical volume element between r text an
I am trying to derive the formula for the area of a sphere using integration It is coming out as pi 2R 2 instead of 4 pi R 2 This is what I am doing I am approximating the area of the So by the usual formula for the surface area of a solid of revolution we want r 02 x 1 dy dx 2dx Find dy dx We get x r2 x2 Square this add 1 bring to a common denominator take the square root So now we need r 02 r xdx r2 x2 The integration is straightforward Either let u r2 x2 or recognize
4 pi r 2
4 pi r 2
https://lh3.googleusercontent.com/proxy/vrTjkyncUjvwZZxMEFtdAkl68hHa1y7RH1sH9vsUsjTHwYosB0ZVvfTFVtkYDkv-kA41DmXHbvkRPB9iuU5sOKptgTAz6oepl2E-byvYqZejQIYNBHlQiAjDDvCDvUnE=w1200-h630-p-k-no-nu

Geometric Formulas Stock Vector Royalty Free 715130806 Multi Step
https://i.pinimg.com/originals/0d/65/d1/0d65d174357dd738d4d347eaf5acc7b4.jpg

Review Of Pre Calculus Calculus Volume 1
https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11213605/CNX_Calc_Figure_App3_002_img.jpg
A r 2 r Intuitively the rate of change of the area of the circle is the circumference Formally A r lim r 0 A r r A r r Now geometrically it is pretty clear but not really easy to prove mathematically that the area of a corona between circles satisfies The volume of a sphere with radius a may be found by evaluating the triple integral V S dxdydz where S is the volume enclosed by the sphere x2 y2 z2 a2 Changing variables to spherical polar coordinates we obtain V 2 0d 0d a 0r2sin dr 2 0d 0sin d a 0r2dr 4 a3 3 as expected Share
Therefore we may write our surface integral as begin align iint Delta S frac mathbf r r 3 d mathbf S int 0 pi int 0 2 pi frac r r 3 r 2 sin theta d phi d theta int 0 pi sin theta d theta int 0 2 pi d phi 2 cdot 2 pi 4 pi end align Therefore the value of the laplacian is zero everywhere except zero What the formula A r2 says is that the area of the circle is larger than the area of the square with side r as you can clearly see by your drawing More precisely the area of the circle is the same as the area of the square with side r because r 2 r2 So what you can say is that the scales the length of the
More picture related to 4 pi r 2
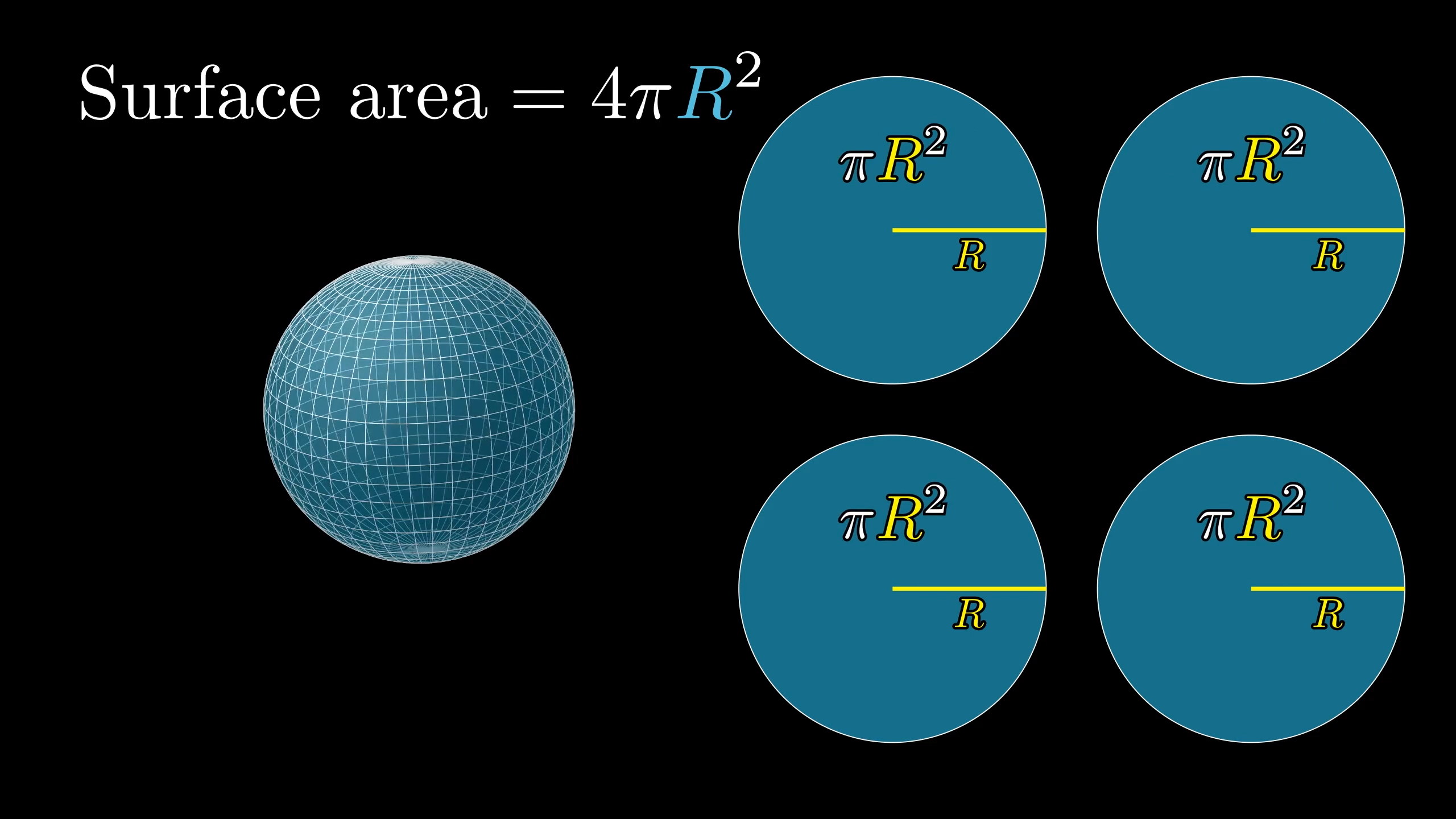
Sphere
https://3b1b-posts.us-east-1.linodeobjects.com/content/lessons/2018/sphere-area/sphere-vs-circles.png

4 Pi R Squared ELSiEiSY Blog
https://i2.wp.com/www.elsieisy.com/wp-content/uploads/2016/02/4-pi-r-squared.jpg?resize=665%2C435&ssl=1
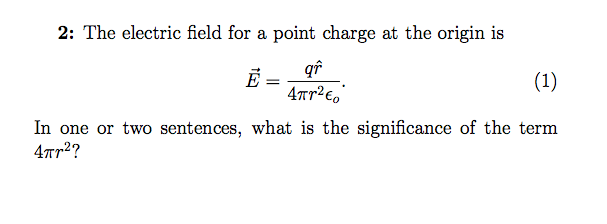
4 Pi R 2 Bobshany
https://d2vlcm61l7u1fs.cloudfront.net/media/2b4/2b45442a-fa56-4544-abb9-81c4715c2569/php39lBsK.png
3 Closed 5 years ago I have absolutely no idea where that formula comes from considering the fact that I am a fifteen year old According to me one way to think of it is to arrange 4 4 circles having radius equal to that of the sphere on it but the curvatures are different so that is not possible Could someone please explain where the 2 pi int R R sqrt R 2 dx 4 pi R 2 Can someone please help me with this one and how the calculation is made Please also explain your approach when solving it
[desc-10] [desc-11]

Answers a P 2x 2r 1 2 Pi R A 1 4 Pi R 2 Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/91e/91ec7873-aaf6-43e7-a14f-a084c221c6bf/phppD8OWP.png

How Surface Area Of A Sphere Is 4 Pi R Squared Easy Explanation In
https://i.ytimg.com/vi/dTvXdtTgn6c/maxresdefault.jpg
4 pi r 2 - What the formula A r2 says is that the area of the circle is larger than the area of the square with side r as you can clearly see by your drawing More precisely the area of the circle is the same as the area of the square with side r because r 2 r2 So what you can say is that the scales the length of the