10 log 10

10 log 10 Help n 2 10 log 3 n 3 10 First of all add 10 on both sides of the equation color white xx log 3 n 3 0 To get rid of the log 3 term you need to exponentiate the expression to the base 3 since a x is the inverse function for log a x and thus both a log a x x and log a a x x hold color white xx

From change of base we have log10 x log10 x ln x ln 10 This we can differentiate as long as we remember that 1 ln 10 is just a constant multipler Doing the problem this way gives a result of y 1 ln 10 1 x Answer link The answer is y log 10 e 1 x Solution Suppose we have log a b we want to change it on exponential e But you can look it up using a calculator for example log102 0 30103 approx Answer link George C May 28 2015 The base 10 logarithm of 2 is the number x such that 10x 2 You can calculate logarithms by hand using just multiplication and dividing by powers of 10 which is just digit shifting and the fact that log10 x10 10

10 log 10

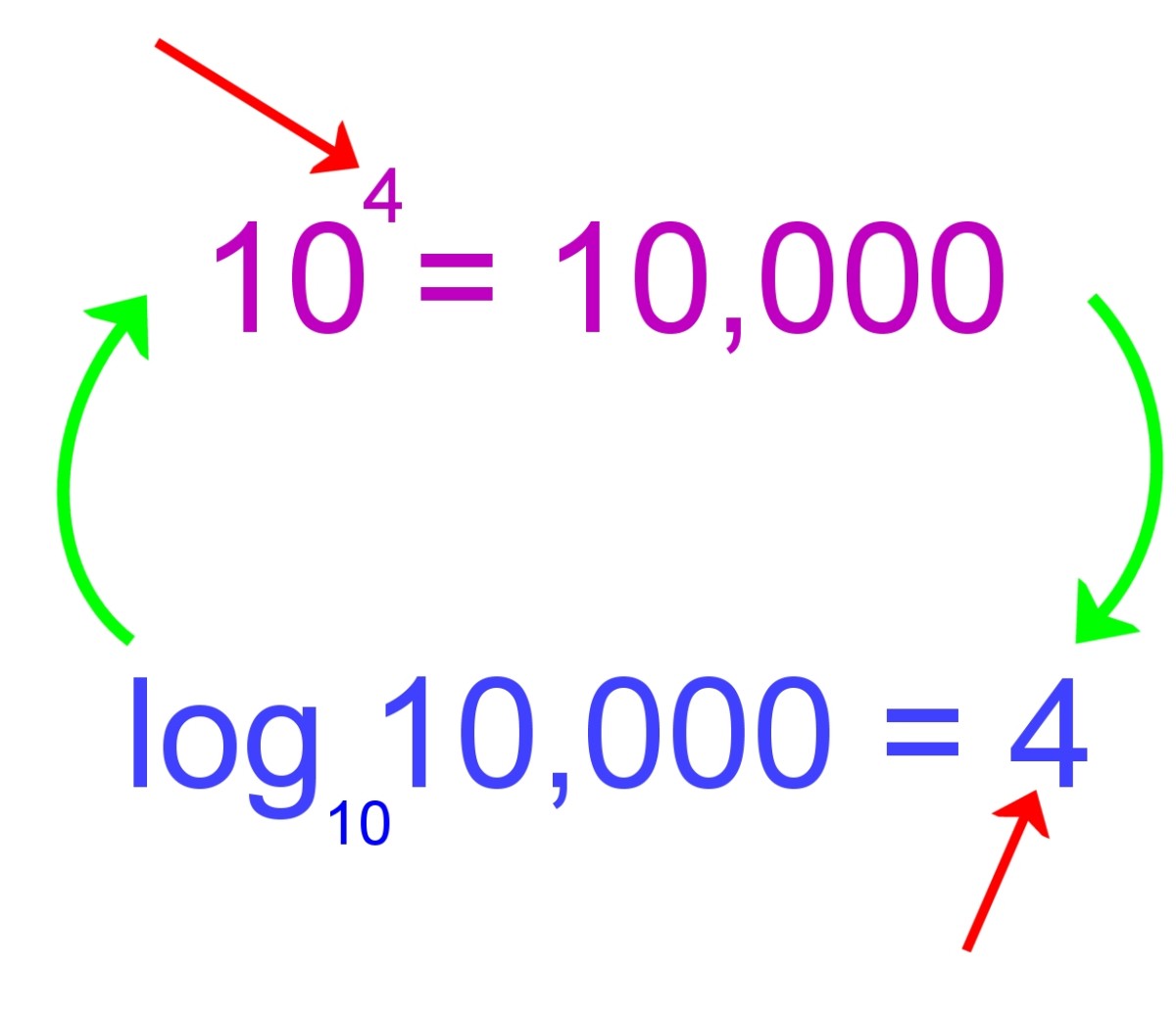
10 log 10
https://images.saymedia-content.com/.image/t_share/MTc0NjM5NzA2NDA2MDA0NzI2/an-introduction-to-logarithms.jpg

log A Log B Log A B Log B A
https://www.meme-arsenal.com/memes/f8d81c817e586ed7fc10b03117e65f6c.jpg

If Log X Base 10 y then Log X 2 Base 1000 Is I Need It Immediately
https://hi-static.z-dn.net/files/d03/07601695af9ca396658ad5fcbe46dea0.jpg

Take 10 to the power of each side of the equation to find that x 1 10 By their definition logarithms have the property that a log a x x Using that we have log 10 x 1 10 log 10 x 10 1 x 10 1 1 10 So x lies between 3 and 4 Using index form first find the log of both sides log 2 x log 10 rArr xlog2 log10 x log10 log2 We know log 10 1 but need to use a calculator to find log2 Using log form this can be written using the change of base rule log 2 10 x x log10 log2 This is the same result as was found the first

Help 10 log pi pi By definition log a is a number such that 10 log a a So in our example 10 log pi pi How do you solve log 10a log 10 a 21 2 Precalculus Solving Exponential and Logarithmic Equations Logarithmic Models 1 Answer

More picture related to 10 log 10

Logs Of Multiples Of 10 Base 10 Calculator TI 84 Calculator
https://i.ytimg.com/vi/XcongXIMVgQ/maxresdefault.jpg

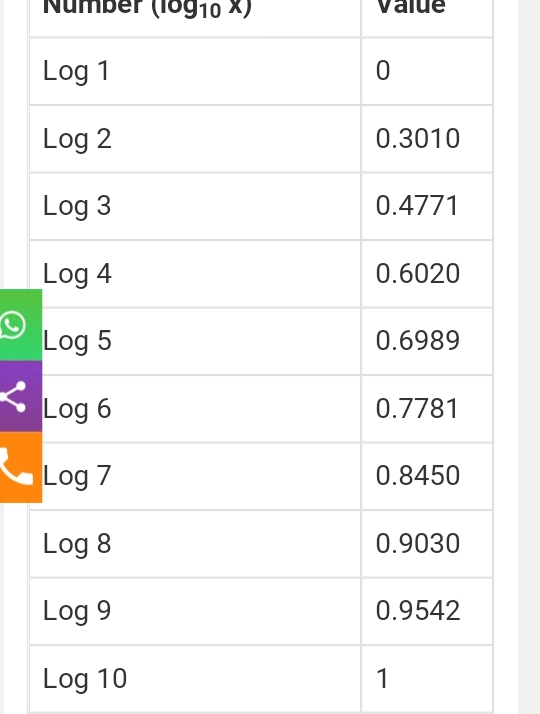
Values Of Log1 To Log 10 Base 10 Mathematics Notes Teachmint
https://teachmint.storage.googleapis.com/public/416551093/StudyMaterial/cd7f896b-38d0-4adc-b1c5-6a3bacd5e401.jpg

Find X In The Following Equation Log 10 x 4 Log 10 x 4 1 YouTube
https://i.ytimg.com/vi/qSN5kIgeSek/maxresdefault.jpg

Hope that helped Answer link Usually log x means the base 10 logarithm it can also be written as log 10 x log 10 x tells you what power you must raise 10 to obtain the number x 10 x is its inverse ln x means the base e logarithm it can also be written as log e x ln x tells you what power you must raise e to obtain the The answer is 5 since 10 5 100 000 However if you just need to find the log of 10 then log refers to log10 just as a radical with no subscript before it indicates it is a square root log10 of 10 is just 1 I assume that you are using log for the Common logarithm that is for the logarithm base 10

[desc-10] [desc-11]

How To Use The Excel LOG10 Function
https://sophuc.com/wp-content/uploads/2020/04/Excel-LOG10-function-1.png

Logarithms And Young s Modulus Revision
https://image.slidesharecdn.com/logarithms-121216133449-phpapp02/95/logarithms-and-youngs-modulus-revision-1-638.jpg?cb=1355664927

10 log 10 - So x lies between 3 and 4 Using index form first find the log of both sides log 2 x log 10 rArr xlog2 log10 x log10 log2 We know log 10 1 but need to use a calculator to find log2 Using log form this can be written using the change of base rule log 2 10 x x log10 log2 This is the same result as was found the first