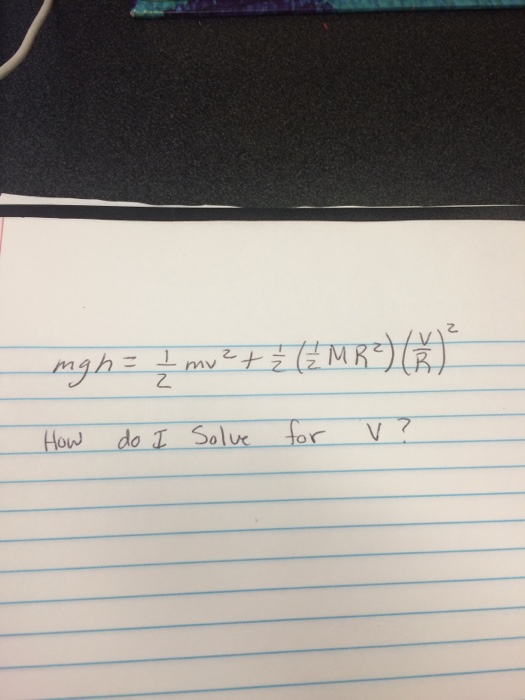1 2mv 2 1 2kt According to the Law of Equipartition of Energy in thermal equilibrium the total energy is distributed equally among all energy modes While the translational and rotational motion contributes KT to the total energy vibrational motion contributes 2 x 1 2KT KT since it has both kinetic and potential energy modes Some Questions for You
What is the equation 1 2mv 2 3 2kT used for in a star cluster This equation known as the equipartition theorem is used to describe the distribution of energy among particles in a system In the case of a star cluster it helps to understand the relationship between the kinetic energy of stars 1 2mv 2 and the temperature of the The temperature of a gas depends on its average kinetic energy avg 1 2mv2 3 2kT In other words the energy of an ideal gas is entirely kinetic The amazing thing about the kinetic molecular theory is that it can be used to derive the ideal gas law
1 2mv 2 1 2kt

1 2mv 2 1 2kt
https://i.ytimg.com/vi/03a2hLu2Q3s/maxresdefault.jpg
Solved Mgh 1 2 Mv 2 1 2 1 2 MR 2 V R How Do I Solve Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/015/015be84d-3a53-48f6-a126-8883b9b9114f/image

https://kenkou888.com/iphone/img/二乗平均速度導出.jpg
The temperature of a gas depends on its average kinetic energy avg 1 2mv 2 3 2kT In other words the energy of an ideal gas is entirely kinetic The amazing thing about the kinetic molecular theory is that it can be used to derive the ideal gas law P V 1 3 N m v 2 The kinetic energy of each molecule is KE 1 2 m v 2 so we can rewrite this as P V 2 3 N 1 2 m v 2 We already know that P V N k T so this means 2 3 N 1 2 m v 2 N k T or 1 2 m v 2 3 2 k T Let us replace our constant speed v with an average speed 1 2 m 2 3 2 k T
So when calculating the temperature of the star s chromosphere do we use the one dimensional kinetic energy E 1 2kT the three dimensional kinetic energy E 3 2kT or the average kinetic energy E kT to equate to 1 2mv 2 where v is the one dimensional velocity Astronomy news on Phys mv2 2kT dv We can evaluate the integral by using the general result that 2s 0 x exp ax2 2s 1 2s 1 as a 1 2 where n indicates a double factorial n n 2 n 4 etc Identifying x v and a m 2kT in our integral above gives 0 v4 exp mv2 2kT dv 3 8 m 2kT 2
More picture related to 1 2mv 2 1 2kt

Let Us Consider An Equation 1 2mv2 Meh Where M Is Mass Of Body V
https://i.ytimg.com/vi/rXHGJR0wYV0/maxresdefault.jpg

Derivation Of KE 1 2mv2 YouTube
https://i.ytimg.com/vi/lSrjahEqAd4/maxresdefault.jpg
https://daigaku-juken.net/wp-content/uploads/2021/09/スライド1-5.jpg
For the simplest collection of particles such as atoms the average kinetic energy is 1 2 m v 2 distributed over the three degrees of freedom where m is the mass and v is the velocity so the total translational energy is 3 2 k B T Doubling the mass of a moving object doubles the energy it has in its kinetic store Doubling the speed of an object increases the energy it has in its kinetic store by four times The energy an object has in its kinetic store of energy is found using the equation Ek mv
Since this is the work done on the object by the force it is equal to the energy transferred to the kinetic energy store of the object In other words it is the energy the object has gained because it is moving its kinetic energy no less Ek mv2 The result above says that the average translational kinetic energy of a molecule in an ideal gas is 3 2 kT For a gas made up of single atoms the gas is monatomic in other words the translational kinetic energy is also the total internal energy

Educational Plan
http://mathpix.com/images/accounts_preview.webp

Solve The Literal Equation K 1 2 mv 2 For V 2 YouTube
https://i.ytimg.com/vi/jGuBgSo_OgE/maxresdefault.jpg
1 2mv 2 1 2kt - 1 2 mv2 kT where k is a proportionality constant v 2kT m If the temperature T is constant and the mass m of a molecule is constant the velocity v must also be constant In the animation above the gas molecules are