1 2 3 2 5 2 n 2 formula In example to get formula for 1 2 2 2 3 2 n 2 they express f n as f n an 3 bn 2 cn d also known that f 0 0 f 1 1 f 2 5 and f 3 14 Then
The series sum limits k 1 n k a 1 a 2 a 3 a cdots n a gives the sum of the a text th powers of the first n positive numbers where a and n are positive integers Each of these series can be calculated through a I have to prove that 1 2 3 2 5 2 2n 1 2 frac n 2n 1 2n 1 3 So first I did the base case which would be 1 1 2 1 2 1 1 2 1 1 3 1 3 3 1 1
1 2 3 2 5 2 n 2 formula

1 2 3 2 5 2 n 2 formula
https://d77da31580fbc8944c00-52b01ccbcfe56047120eec75d9cb2cbd.ssl.cf6.rackcdn.com/c0d76e7b-ceac-402f-99b6-80c96fabc3fa/slide42.jpg

48 1 2 2 2 KUROKAWAONSEN MAIN JP
https://i.stack.imgur.com/gkQWr.png
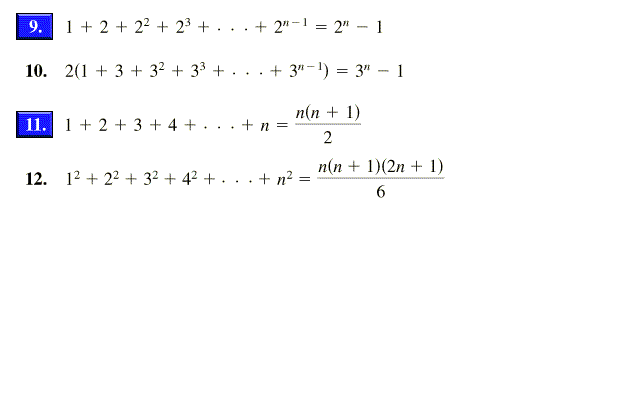
2n 1 Formula
https://media.cheggcdn.com/study/4ae/4ae74c4c-61fe-4b46-ba61-1177938b9112/2007517165735633150178555300000977.png
Program for finding the sum of the nth term of the series n 2 1 2 2 n 2 2 2 3 n 2 3 2 n n 2 n 2 Examples Input 2 Output 3 Input 5 Output 150 To solve this If n is a positive integer show that 1 nn 1 n n 1 n 1 n n 1 2 n 2 n 1 1 2n n 1 2 nn n 1 n 1 n n 1 n 2 n 2 n 1 the series in each case being extended to n
N n 2 5 is divisible by 6 for each natural number n Prove the statement by using the Principle of Mathematical Induction n 2 2 n for all natural numbers n 5 A sequence b 0 b 1 b 2 is How to prove a n n for all n sufficiently large and n leq n n for all n by induction 3 Given frac a b c d frac a b c d show that a 2 b 2 c 2 d 2 ac bd 2
More picture related to 1 2 3 2 5 2 n 2 formula

2 2 3 2 5 2 n 0 125 27 Brainly in
https://hi-static.z-dn.net/files/d4f/cfa4cfdc7f596fad18c0fef447d3be7d.jpg

Proving 1 5 9 13 4n 3 2n 2 n BY INDUCTION YouTube
https://i.ytimg.com/vi/6ulF2pIvS6U/maxresdefault.jpg

10 Chapter 3 Test Form 2B ShanelleCalla
https://d1avenlh0i1xmr.cloudfront.net/dd89c55b-6272-4caf-b866-de6259e85053/slide49.jpg
In Exercises 1 15 use mathematical induction to establish the formula for n 1 1 12 22 32 n n 1 2n 1 n2 6 Proof 1 2 3 For n 1 the statement reduces to 12 and is Example 1 For all n 1 prove that 12 22 32 42 n2 n n 1 2n 1 6 Let P n 12 22 32 42 n2 1 2 1 6 Proving for n 1 For n 1 L H S 12 1 R H S 1 1 1 2 1 1 6 1
SumofSquaresOfOddNumbers SumOfSquares OddNumbers IIT JEE NMTC NTSE PERMO RMO INMOFormula to find the sum of squares of first n odd numbersLink to t In summary the formula for 1 2 2 2 3 2 n 2 is n 6 n 1 2n 1 which can be proved by induction using the telescoping property of k 1 3 k 3 and the known

2 4 16 4 16 2 5 2 Brainly lat
https://es-static.z-dn.net/files/d42/e17496a32051126d24fbedb921989667.jpg

Solved Here Are A Couple Of Formulas Sigma i 1 n 2i 1 Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/2a9/2a9c9050-79cf-4e76-8603-17035b1a2963/phpYsZGBZ.png
1 2 3 2 5 2 n 2 formula - Symbolab equation search and math solver solves algebra trigonometry and calculus problems step by step