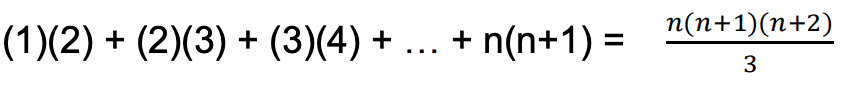1 2 2 3 3 4 n n 1 formula The series sum limits k 1 n k a 1 a 2 a 3 a cdots n a gives the sum of the a text th powers of the first n positive numbers where a and n are positive integers Each of these series can be calculated through a
begingroup n 1 3 n 3 3n 2 3n 1 so it is clear that the n 2 terms can be added with some lower order terms attached by adding the differences of cubes giving a leading Ex 4 1 2 Prove the following by using the principle of mathematical induction 13 23 33 n3 1 2 2 Let P n 13 23 33 43 n3 1 2 2 For n 1 L H S 13 1 R H S 1 1 1 2 2
1 2 2 3 3 4 n n 1 formula
1 2 2 3 3 4 n n 1 formula
https://media.cheggcdn.com/media/1c3/1c3abe40-0e73-44b1-b567-624880852c50/phpYus1jP

1 3 YouTube
https://i.ytimg.com/vi/mzwq2N_DKt0/maxresdefault.jpg

2 1 2 WAFER BFLY DI NBR F W HAIT DA ACT Pneumatic Actuated Butterfly
https://cdn.pimber.ly/public/asset/raw/5ee8a13150af727432f87049/306f1247/61c1b3bfd58d233bc00001f0/IFT-M331-08481W-large1425.png?w=3840&q=100
Try to make pairs of numbers from the set The first the last the second the one before last It means n 1 1 n 2 2 The result is always n And since you are adding In order to transform the series 1 2 3 4 into 1 2 3 4 one can subtract 4 from the second term 8 from the fourth term 12 from the sixth term and so on The total amount to
Let n n 2 n 3 n 4 cdot cdot cdot n n Sum Then 1 n n 2 n 3 n 4 cdot cdot cdot n n Sum 1 n times 1 n n 2 n 3 n 4 cdot cdot cdot n n N 1 1 2 1 3 1 4 1 n Unlike the geometric series the harmonic series does not converge but it diverges as we add more terms The partial sums of first n terms can
More picture related to 1 2 2 3 3 4 n n 1 formula
Solve The System Ax B Using The Given LU Factorizat SolvedLib
https://cdn.numerade.com/previews/bae2d537-6e8f-4cf3-bb70-3e999434d1c9_large.jpg

1 2 2 4 3 8 N 2n 2 N 2 2 N Id Free Download Nude Photo Gallery
https://id-static.z-dn.net/files/d0a/81607d8a4b29ea934afcb236ae9b2f97.jpg

Limit N 1 4 2 4 3 4 n 4n 5 Limit N 1 3 2 3 3 3 n 3n 5
https://d1hj4to4g9ba46.cloudfront.net/questions/1118007_1025137_ans_0e2cfc976c7f4bb8bb9f3ef0fe19541e.jpg
If k n 1 2 then you can calculate easily the smallest and largest i such that n i k using integer division and from that you can count how many such i there are multiply by k and you get the sum of n i for all these i There exists a formula for the n th term of this sequence A002024 from the OEIS n appears n times 1 2 2 3 3 3 4 4 4 4 5 which is 1 1 8n 2 Is there a better
Given an integer n the task is to find the sum of the series 1 1 2 2 3 3 n n using recursion Examples Input n 2 Output 5 1 1 2 2 1 4 5 Input n 3 This is what I ve been able to do Base case n 1 L H S 1 3 1 R H S 1 2 1 Therefore it s true for n 1 I H Assume that for some k in Bbb N 1 3 2 3

Solve The Following Equation X 6 1 2 3x X 3 3 2x X 2 0
https://d1hj4to4g9ba46.cloudfront.net/questions/1560347_1705736_ans_351a267b8a86423caee42427016e1f7f.jpg
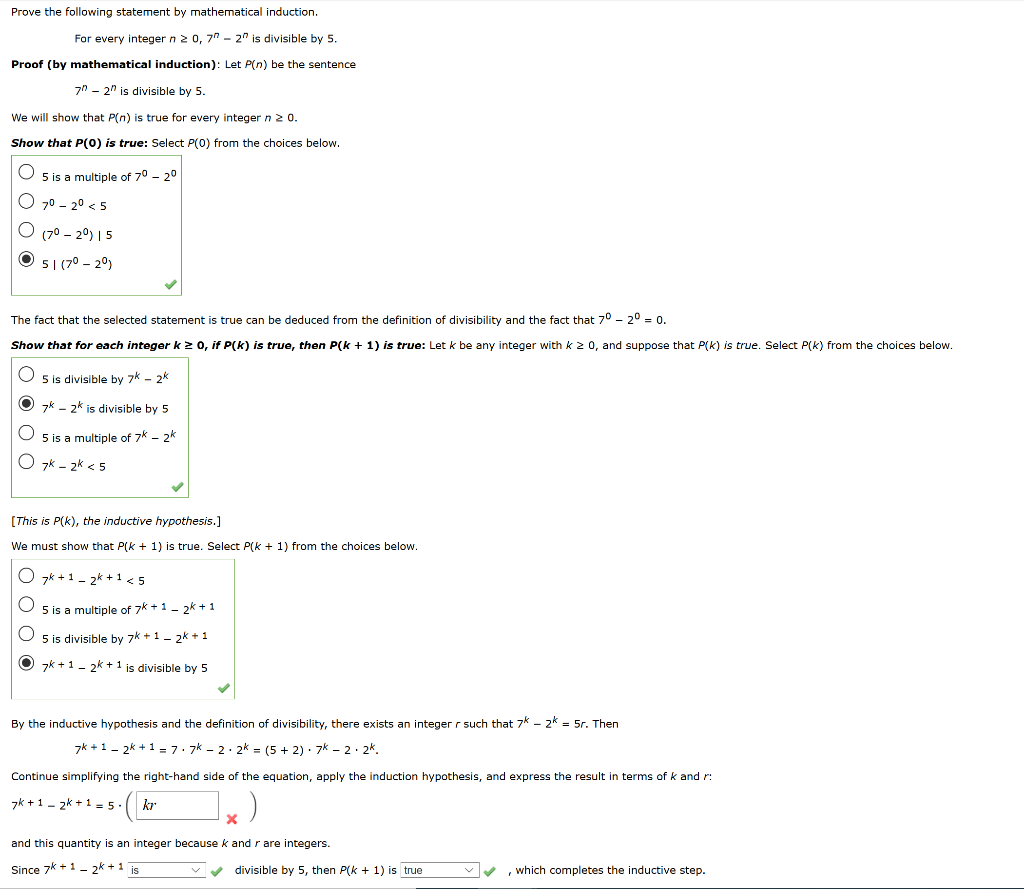
Solved Prove The Following Statement By Mathematical Chegg
https://media.cheggcdn.com/media/771/771442d1-8154-455d-a16b-ed0f60f0d7ad/phpZcSvNL.png
1 2 2 3 3 4 n n 1 formula - Let n n 2 n 3 n 4 cdot cdot cdot n n Sum Then 1 n n 2 n 3 n 4 cdot cdot cdot n n Sum 1 n times 1 n n 2 n 3 n 4 cdot cdot cdot n n