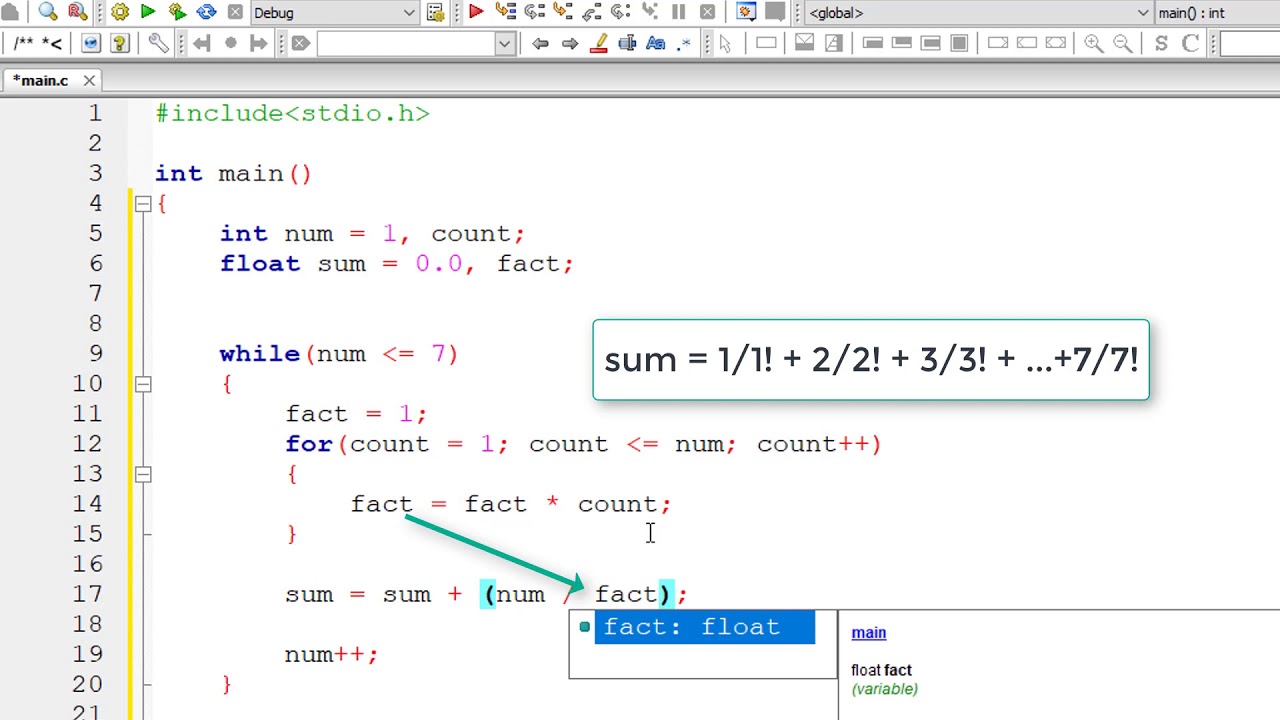
1 1 2 2 3 3 n n formula Sum of the series 1 1 2 2 3 3 n n using recursion Last Updated 22 Sep 2022 Given an integer n the task is to find the sum of the series 11 22 33 nn using recursion Examples Input n 2 Output 5
How to calculate this series Sn 1 1 2 2 3 3 n n where n 1 First you need parenthesis just like you do in math if you want to be sure to get the expected result And you d be pleased to know math is not English based it s the universal language In example to get formula for 1 2 2 2 3 2 n 2 they express f n as f n an 3 bn 2 cn d also known that f 0 0 f 1 1 f 2 5 and f 3 14 Then this values are inserted into fu
1 1 2 2 3 3 n n formula

1 1 2 2 3 3 n n formula
https://i.stack.imgur.com/v3q1A.png
C Program To Find Sum Of Series 1 1 2 2 3 3 N n YouTube
https://i.ytimg.com/vi/Nok-OqhKpDY/maxresdefault.jpg

Prove That 1 3 2 3 3 3 N 3 n n 1 2 2 Teachoo
https://d77da31580fbc8944c00-52b01ccbcfe56047120eec75d9cb2cbd.ssl.cf6.rackcdn.com/35fc8831-5164-4361-8f62-33b2ed06e0a2slide7.jpg
He provides courses for Maths Science and Computer Science at Teachoo Ex 4 1 2 Prove the following by using the principle of mathematical induction 13 23 33 n3 1 2 2 Let P n 13 23 33 43 n3 1 2 2 For n 1 L H S 13 1 R H S 1 1 1 2 2 1 2 2 2 1 2 1 Hence L H S R H S P n is Sum of the series 1 1 2 2 3 3 n n using recursion in C In this problem we are given a number n which defines the nth terms of the series 1 1 2 2 3 3 n n Our task is to create a program that will find the sum of the series
The implementation there is slightly buggy but the idea is there The key strategy is to find x such that n x 1 m and repeatedly reduce n n m to n x m n x n n x m I am sure this strategy works The series sum limits k 1 n k a 1 a 2 a 3 a cdots n a gives the sum of the a text th powers of the first n positive numbers where a and n are positive integers Each of these series can be calculated through a closed form formula
More picture related to 1 1 2 2 3 3 n n formula

1 1 2 2 3 3 N n n 1 1 E itli inin Ispat YouTube
https://i.ytimg.com/vi/VTpz4GHz8gA/maxresdefault.jpg

2 1 2 WAFER BFLY DI NBR F W HAIT DA ACT Pneumatic Actuated Butterfly
https://cdn.pimber.ly/public/asset/raw/5ee8a13150af727432f87049/306f1247/61c1b3bfd58d233bc00001f0/IFT-M331-08481W-large1425.png?w=3840&q=100
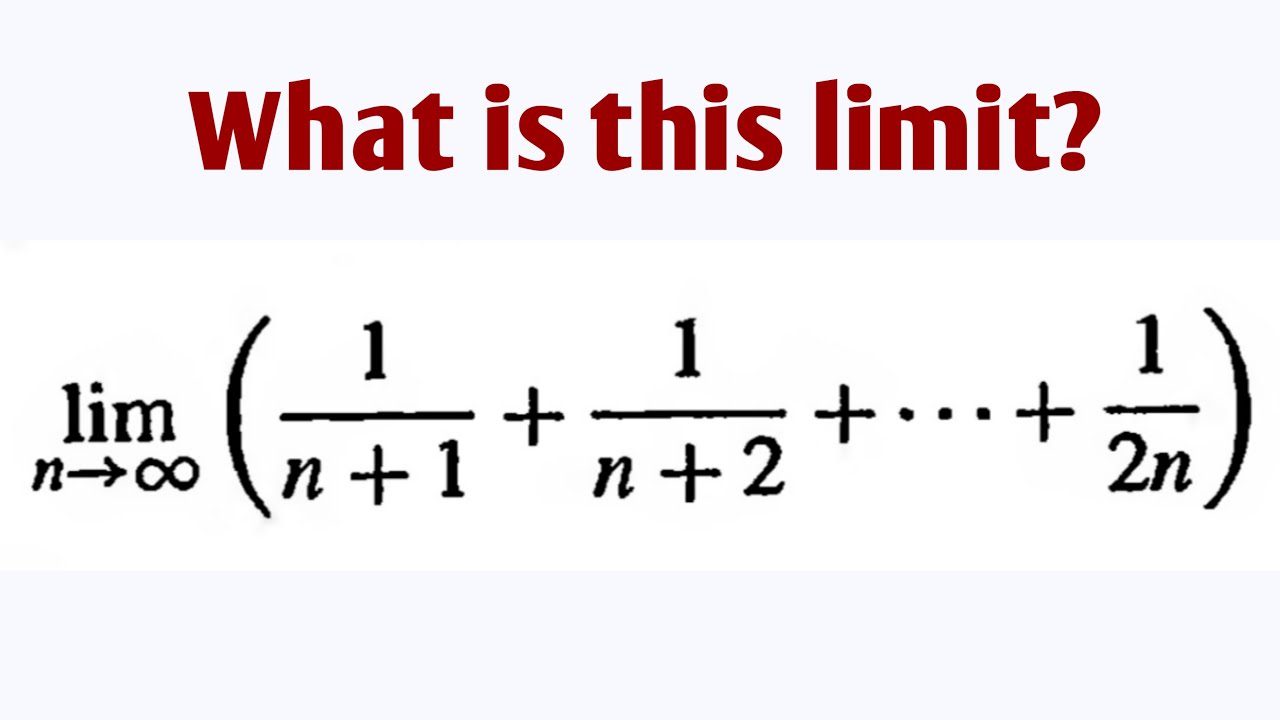
Lim 1 n 1 1 n 2 1 2n What Is This Limit YouTube
https://i.ytimg.com/vi/JPLri-Dj7ag/maxresdefault.jpg
This is what I ve been able to do Base case n 1 L H S 1 3 1 R H S 1 2 1 Therefore it s true for n 1 I H Assume that for some k in Bbb N 1 3 2 3 k 3 It means n 1 1 n 2 2 The result is always n And since you are adding two numbers together there are only n 1 2 pairs that can be made from n 1 numbers
[desc-10] [desc-11]

Prove The Following By Using The Principle Of Mathematical Induction
https://www.shaalaa.com/images/_4:02564466db60430a83b978a4af50385d.png
Solve The System Ax B Using The Given LU Factorizat SolvedLib
https://cdn.numerade.com/previews/bae2d537-6e8f-4cf3-bb70-3e999434d1c9_large.jpg
1 1 2 2 3 3 n n formula - The implementation there is slightly buggy but the idea is there The key strategy is to find x such that n x 1 m and repeatedly reduce n n m to n x m n x n n x m I am sure this strategy works